Introduction

In the past couple of years, the development of large language models (LLM) has taken the world by storm. Models such as OpenAI’s GPT-4 have demonstrated performances surpassing humans on many natural language related tasks. However, since the early days of the release of these LLMs, accessibility to the general public was limited. This was mainly for two reasons. The first is that the flagship generative AI company OpenAI did not (and still does not) release any of the weights or the training data used for models later than GPT-2. The second reason is that even with the release of many open source models beginning in the latter half of 2023, the compute costs for training such models remained prohibitive for the average consumer. For reference, the GPT-3 model contained 175 billion parameters, which meant that even storing such a model on a device was beyond most people’s hardware, much less training it.

There have been some open source models such as Falcon-40B that have claimed to be competitive with GPT-3 on certain tasks. However, it seems that the consensus is that a good open domain LLM must be at least around 65 billion parameters, and that smaller models can only be used for very specific tasks. Researchers and corporations may have access to greater compute resources, but even if they had all the GPUs they needed to fine-tune the models, the monetary costs (and the carbon footprint) would be astronomical. Therefore a more efficient method of training large language models had to be used.

In this post, we will discuss the newest state-of-the-art method of parameter efficient fine-tuning, called RoSA.

Parameter Efficient Fine-Tuning

In recent years, the area of parameter efficient fine-tuning (PEFT) has exploded in popularity due to precisely the demands of LLMs. This is a large area with many differing approaches. More traditional techniques include quantization and pruning, and these are still useful, but in this post we will focus more on how to massively reduce the number of training parameters. The difference such techniques can bring is significant. With techniques such as LoRA, certain models can now be fine-tuned on a commercial GPU such as the NVIDIA RTX 3090.

Let us detail this idea in more concrete terms. Let \(\theta^D\) be the weights of a model \(f(x, \theta)\) which has \(D\) parameters, with \(D\) typically being very large. Then let \(\theta^D_0\) denote the original weights of the model. Traditionally, training the model meant doing a gradient update over all \(D\) parameters

\[\theta^D = \theta_0^D + \nabla\theta^D_0\]

Here we see the problem: whatever hardware the model is running on must have enough space to store both the original models and the gradients, which are just as large as the original parameters!

What can be done to reduce the amount of storage used? Assuming we don’t want to change the original model to a smaller one (e.g. distillation), we must try to reduce the dimensionality of the gradients.

Intrisic Dimension

In 2020, researchers1 discovered a key insight in training language models: even though there is a large number of trainable weights, call this number \(D\). The weights can be projected onto a smaller subspace and still achieve almost comparable performance as training the original weights. In other words, a subset of the original weights can encode enough information about the model to learn just as much as the original set of weights. Then smaller subset of weights lie in a smaller dimension \(d << D\), and the researchers call this the intrinsic dimension of the model.

Revisiting the equation in the last section, the idea is to optimize over the smaller subspace then project onto the original weight space. Here the dimension of the subspace is assumed to be much smaller

\[\theta^D = \theta_0^D + P(\nabla\theta^D_0)\]

where \(P: \mathbb{R}^d \rightarrow \mathbb{R}^D\) is a projection operator. Here we see that if this training procedure can be carried out, then the hardware will only need to store \(D + d\) parameters instead of the original \(2D\) parameters. The authors chose the Fastfood transform2 for the operator \(P\), although in principle there is no “best” operator for such a task.

Unfortunately there is no formula for actually computing the intrisic dimesion of a model. The authors simply compare the performance of the model across different candidate dimensions \(d\) until they have reached a satisfactory value. The threshold for a satisfactory performance is defined to be at least 90% of the score of the original model.

In addition, the authors prove generalization bounds related to the intrisic dimesion \(d\). This gives further evidence that large models can be compressed to a much smaller dimension.

LoRA

Now we introduce what has pretty much become the industry standard PEFT method. Low-rank Adaptation (LoRA) was a landmark paper written in 2021 before the surge of LLMs, but industry experts quickly caught onto it as the key algorithm to reduce memory footprint.

LoRA takes inspiration from the intrisic dimensionality paper and define their own operator for the gradient updates. Given the paramter update equation

\[\theta^D = \theta_0^D + \nabla\theta^D_0\]

the authors decompose the gradient matrix into 2 lower rank matrices \(\nabla\theta^D_0 = BA\) where \(B \in \mathbb{R}^{d \times r}\) and \(A \in \mathbb{R}^{r \times k}\) both have rank \(r\). Translated into the framework of the intrisic dimensionality paper: The original dimension of the model is \(d \cdot k\), the intrisic dimension of the model is \(d_i := r(d+k)\) for \(r << \min(d, k)\), and the operator \(P\) is given by \(P(\theta^{d_i}) = P_B\theta^{d_i} P_A\theta^{d_i}\) where \(P_A, P_B\) are projection operators to subspaces \(\mathbb{R}^{kr}, \mathbb{R}^{dr}\) respectively.

It turns out that there is a lot of compressibility in transformer-based models, with the intrisic dimension being less than 1% of the original dimension.

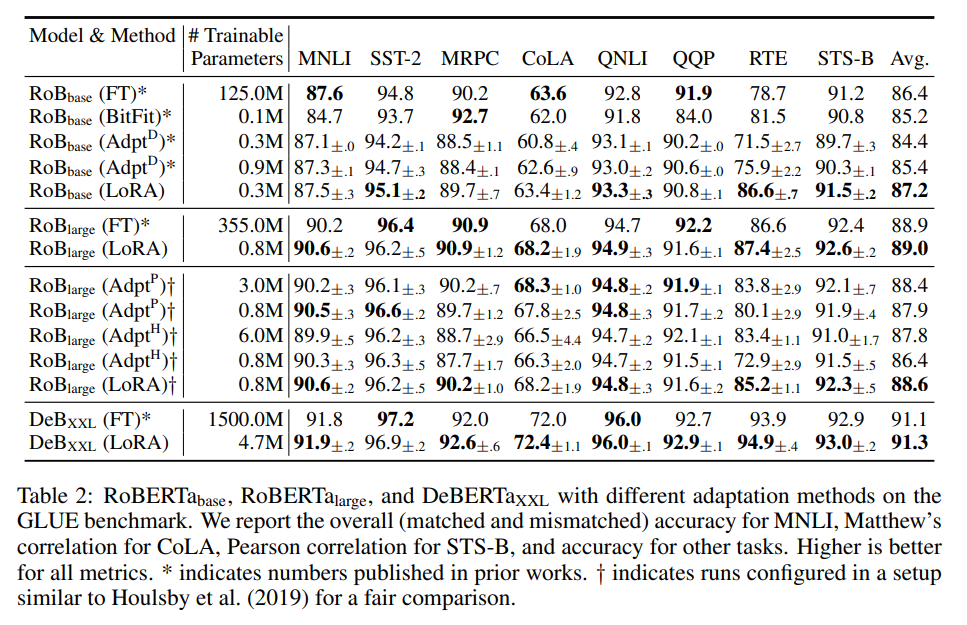Empirical results from the LoRA paperEmpirical results from the LoRA paper 3

Additionally, applying LoRA on GPT-3 shows it to be competitive with the baseline full fine-tuning method on tasks such as WikiSQL and MultiNLI-matched. This raises hope that we can save several orders of magnitude on training parameters without sacrificing any accuracy!

Low-Rank Decomposition and Principal Component Analysis

Of course, the ideal scenario is for the matrix \(\nabla\theta^D_0\) to be decomposable into matrices \(B, A\), so that no information is lost and we preserve perfect accuracy. However, that is not always possible, and in the absense of a perfect low-rank decomposition, we are left with minimizing the difference between \(\nabla\theta^D_0\) and the product \(BA\). Therefore the LoRA paradigm is essentially a version of a very old optimization problem:

\[\text{min}_C ||\nabla\theta^D_0 - C||_F^2 \quad\text{ s.t. rank}(C) \le r\]

The observant reader may have noticed similarities to another common ML algorithm: Principal Component analysis (PCA). Recall that the PCA problem for a data matrix \(X\) can be solved via a singular value decomposition (SVD) approach. Namely, decompose \(X = U \Sigma V^T\) where \(U, V\) are orthogonal and \(\Sigma\) is diagonal. The singular values will simply be the values of the diagonal matrix \(\Sigma\). Then, the connection to low-rank decomposition is given by the Eckart-Young-Minsky theorem:

Theorem (Eckart, Young, Minsky) Given a matrix \(X\) with its SVD \(X = U \Sigma V^T\). The truncation matrix \(X_k\) solves the optimization problem

\[\text{min}_B ||X - B||_F^2 \quad\text{ s.t. rank}(B) = k\]

With this formulation, we can see that LoRA can be seen as a (very high dimensional) version of PCA. As such, it is susceptible to the same drawbacks as PCA, one of which is sensitivity to outliers (due to the optimization problem involving the Frobenius norm).

Sparse Plus Low-Rank Decomposition

The remedy to the drawbacks in the previous section is to decompose a matrix \(W\) into a sum

\[W = L + S\]

Where \(L\) is low rank and \(S\) is sparse. This way, the low rank matrix \(L\) captures the principal components of the matrix, and \(V\) captures the corruptions of the matrix (i.e. outliers).

Let’s illustrate this decomposition with a simple example.

\[\begin{pmatrix} 1 & 0 & -1\\ 1 & 6 & -4\\ 3 & 9 & -9 \end{pmatrix} = \underbrace{ \begin{pmatrix} 1 & 0\\ 0 & 2\\ 3 & 3 \end{pmatrix} \begin{pmatrix} 1 & 0 & -1\\ 0 & 3 & -2 \end{pmatrix} }_{L, \hspace{0.1cm} rank(L) \le 2} + \underbrace{ \begin{pmatrix} 0 & 0 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix} }_{S, \hspace{0.1cm} ||S||_0 \le 1}\]

here the intrisic dimension is 2 and the sparsity density is \(1/9\). Notice that we also decomposed the low rank component into the product of 2 matrices as in the LoRA setup. This suggests that our original matrix is almost rank 2, but there is a small “corruption” in its data which makes it full rank.

RoSA

Robust Sparse Adaptation (RoSA)4 is a new PEFT method which leverages the sparse component of the weight matrix as well as the low rank component. More concretely, the weight update equation is now:

\[\theta^D = \theta_0^D + (S + BA)\]

where \(B \in \mathbb{R}^{d \times r}\) and \(A \in \mathbb{R}^{r \times k}\) both have rank \(r\) AND \(S\) is a sparse matrix (implemented in CSR format) with Frobenius norm bounded above by \(\rho \cdot d \cdot k\). Here \(\rho < 1\) is the perturbation density controlling the sparsity of \(S\).

(Notice the addition of a new matrix compared to LoRA)

In the actual implementation of calculating gradients, the authors employ a fixed sparsity masking layer to only update a the fraction of components of the sparse matrix dictated by the perturbation density. The masking layer is computed as follows:

  1. Select a small subset of the training data
  2. Run the training loop and accumulate gradients
  3. Pick the top \(\rho \cdot d \cdot k\) components of the gradient matrix (in absolute value) to be the masking layer

In the previous section, we noted that PCA can be very sensitive to outliers. In a similar vein, the authors of RoSA show through experiments that LoRA training performs badly on certain complex tasks such as the ViGGO dataset and the GSM8k dataset. Indeed they pick a random layer in the LLM and exhibit the prescence of singular values (i.e. outliers). This suggests that only employing the low rank component of the weight matrix may not be sufficient for more complex downstream tasks.

To gain a better intuition for this phenomeon, let us briefly consider another major application of low rank + sparse decomposition of matrices – video surveillance. In the image below, the first column represents the original image, the second column represents the low rank component, and the third column the sparse component.

Experiments on video surveillance footageExperiments from 5

By this analogy, the LoRA approach will filter out crucial information such as the 3 people close to the camera in the first image. We can think of the complex downstream tasks such as ViGGO to be complex images like the frame in the top row, where both low rank and sparse information are needed. Similarly, we can think of datasets like WikiSQL (which LoRA performed well on) to be analogous to the surveillance footage with only the lone person in the background (so the sparse component will be negligible).

At this point, the observant reader might point out that while accuracy has been improved by adding sparse components, wouldn’t this increase the total number of parameters, thereby defeating the whole purpose of PEFT? This would be true if we simply added sparse components to the existing low rank matrices given by LoRA, BUT because the sparse components have added critical information to the model, we can also lower the rank! Indeed, the authors of RoSA have found the best models to have a rank lower than those found by LoRA. The result is that the total number of parameters have actually been lowered, even with the additional sparse components.

Conclusion

To summarize the post, RoSA is a new cutting-edge PEFT method which takes the classic problem of sparse + low-rank decomposition of matrices, and completes the sparsity half that was missing from the LoRA approach.

  1. Armen Aghajanyan, Luke Zettlemoyer, and Sonal Gupta: Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning http://arxiv.org/abs/2012.13255. (2020) ↩

  2. Quoc Le, Tamas Sarlos, and Alex Smola. Fastfood-approximating kernel expansions in loglinear time. Proceedings of the international conference on machine learning, volume 85 (2013) ↩

  3. Edward Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, Weizhu Chen LoRA: Low-rank Adaption of Large Language Models ↩

  4. Mahdi Nikdan, Soroush Tabesh, Elvir Crncevic, Dan Alistarh. RoSA: Accurate Parameter-Efficient Fine-Tuning via Robust Adaptation (2024) ↩

  5. Emmanuel J. Candes, Xiaodong Li, Yi Ma, John Wright. Robust Principal Component Analysis? (2009) ↩